만약 글을 읽는 분께서, 돈과 관련된 업무 또는 정확한 수치를 기반으로 진행해야 하는 업무를 맡게 된다면 어떻게 하시겠습니까?
float이나 double을 해답으로 생각하셨다면 한번 이 글을 통해 더 나은 방법에 대해 같이 고민해보는게 좋을 것 같습니다.
float과 double의 문제점
float과 double은 연산했을 때, 나오는 가장 유명한 문제 입니다.
코드는 java를 기준으로 작성되었습니다.
public class FloatTest {
public static void main(String[] args) {
float a = 0.1f;
float b = 0.2f;
if(a + b == 0.3){
System.out.println("a + b == 0.3");
}
System.out.println("a + b != 0.3");
}
}
이 코드를 실행하게 되면 a+b != 0.3 이라는 결과를 출력하게 됩니다.
만약 a,b 변수를 double로 변경해도 똑같은 결과를 출력하게 됩니다.
왜 이런걸까요?
- float과 double이 정확한 값(precise value)가 아닌 근삿값(approximate value)을 담고 있어서 발생하는, 부동소수 타입의 대표적인 문제입니다. 그렇다면 문제에 대한 근본적인 원인을 파악하기 위해 고정소수점과 부동소수점에 대해 간략하게 알아보겠습니다.
고정소수점과 부동소수점
- 고정 소수점 표현방식(fixed point number representation)
고정소수점 표현방식은 실수를 부호 비트(signed bit), 정수부(integer part)와 소수부(fractional part)로 나누고,자릿수를 고정하여 실수를 표현하는 방식입니다.
- 예를 들어 7.75라는 실수를 2진수로 변환하면 111.11이 됩니다. 이를 각각 지수부와 소수부에 담아 표현합니다( 그림은 32비트 기준입니다)
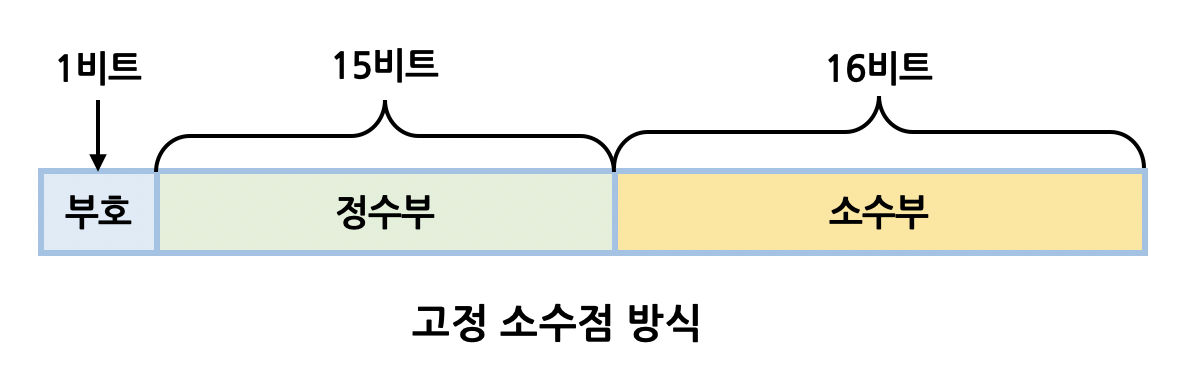

고정소수점 표현방식은 구현 방법이 간단하다는 장점이 있지만, 자릿수가 제한되어 있으므로 표현할 수 있는 수의 범위가 한정적이라는 단점이 있습니다. 이에 따라 더 넓은 범위의 실수를 표현하기 위해 부동소수점이라는 개념이 등장했습니다.
2. 부동소수점 표현방식(floating point number representation)

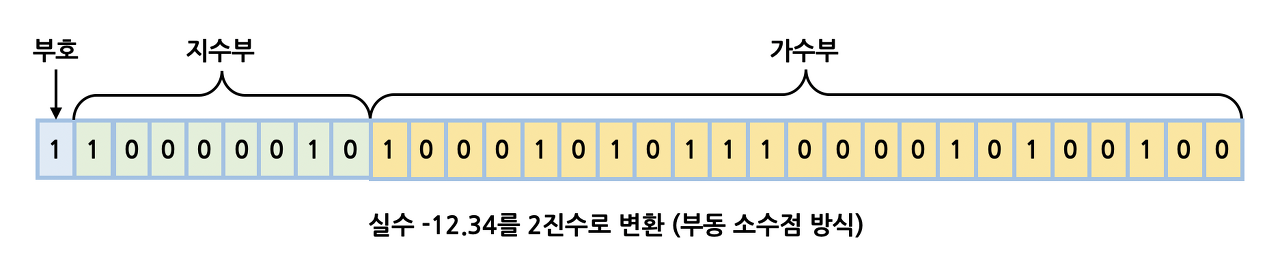
부동소수점 표현방식은 실수를 부호부(sign), 지수부(exponent), 가수부(mantissa)로 나누고, 정규화된값을 각 비트에 나눠 담아 실수를 표현하는 방식입니다. 쉽게 말해 12.3456을 저장한다면 표현식을 0.123456 * 10^2로 변경한 다음, 가수부에는 0.123456을 담고 지수부에는 2를 저장하는 방식입니다.
(실제로는 IEEE 754 표준에 따라서 지수부에 bias라는 값을 더해주는 과정을 거치게 됩니다.)
부동소수점 표현방식은 고정소수점 표현방식에 비해 표현 범위가 더 넓지만, 근본적으로 2진수를 사용하므로 여전히 소수를 표현할 때 오차가 발생하게 됩니다. 예를 들어 0.3을 2진수로 변환하면 0.0100100100…처럼 특정 수가 무한적으로 반복됩니다. float과 double이 이와 같은 부동소수점 표현방식으로 구현되었기 때문에 앞선 문제들이 발생한 것 입니다.
이런 문제를 해결하기 위해 자바에서는 BigDecimal 클래스를 제공합니다.
BigDecimal이란?
공식문서에서 BigDecimal은 불변의 성질을 띠며, 임의 정밀도와 부호를 지니는 10진수라고 표현합니다. 임의 정밀도(arbitary-precision)란 쉽게 말하자면 아무리 큰 숫자라도 표현할 수 있는 것을 의미합니다.(실제로는 무한에 가까울 뿐 무한은 아닙니다.)임의 정밀도 연산은 플랫폼마다 구현에 차이는 있지만 기본적으로 큰 숫자를 배열에 나눠 담는 방식으로 구현됩니다.
1231235451235 = [1]+[2]+[3]+[1]+.....
BigDecimal은 내부적으로 임의 정밀도 연산을 활용하는 동시에 불변이므로 BigDecimal 객체 간의 연산마다 새로운 객체를 생성합니다. 이에 따라 float나 double 과 같은 기본 타입에 비해 사용하기 훨씬 느리며, 사용방법도 어렵습니다. 물론 int나 long이라는 대체제가 있지만, 실수를 표현할 수 없고 값의 범위가 비교적 제한된다는 점 때문에 BigDecimal은 금융 관련 계산에서 필수적으로 사용됩니다.
BigDecimal의 구성
BigDecimal은 개념적으로 임의 정밀도 정수형인 unscaled value와 소수점 오른쪽의 자릿수를 나타내는 32비트 정수인 scale로 구성됩니다.
- 예를 들어 BigDecimal 3.14의 경우 unscaled value는 314이고, scale은 2가 됩니다.
내부적으로 살펴보면 intVal, scale , precision , intCompact 로 구성되어 있습니다.
- intVal은 BigInteger 타입으로서 unscaled value를 저장하는 변수입니다.
- scale은 소수점 오른쪽의 자릿수
- precision은 총 자릿수를 나타냅니다.
또한 특이한 점으로는 intCompact가 long 타입으로 선언되어 있다는 것인데, 만약 값의 크기가 작아서 유효숫자의 절댓값이 long타입으로 표현될 수 있다면 BigDecimal은 unscaled value를 intVal 대신 intCompact에 저장함으로써 메모리를 최적화합니다.
package java.math;
public class BigDecimal extends Number implements Comparable<BigDecimal> {
private final BigInteger intVal; // = unscaled value
private final int scale;
private transient int precision;
private final transient long intCompact;
...
이외에도 BigDecimal클래스 사용법에 대해 알고 싶은 분은 참고 자료를 참고해주세요
참고 자료
'프로그래밍 > Java' 카테고리의 다른 글
| Java volatile이란? (0) | 2023.09.08 |
|---|---|
| 함수형 프로그래밍 (0) | 2023.04.11 |
| G1 GC에 대해 (0) | 2023.03.31 |
| Singleton 패턴과 스프링에서는 Singleton 패턴을 어떻게 사용하고 있을까? (1) | 2023.01.27 |
| Long 과 AtomicLong은 어떤 차이가 있을까? (0) | 2023.01.24 |