시간 복잡도
시간 복잡도는 주어진 문제를 해결하기 위한 연산 횟수를 말합니다. 일반적으로 수행 시간은 1억번의 연산을 1초의 시간으로 간주하여 예측합니다.
- 평균 성능을 가진 컴퓨터(CPU)로 사칙연산에 대한 속도를 측정해보면 1초에 약 8.5 X $10^7$(회), 즉 8,500만 회의 연산을 수행합니다
- 따라서 CPU가 1초에 수행가능한 연산의 횟수를 1억번으로 간주하여 예측하는 것 입니다.
시간 복잡도를 정의하는 방법
- 빅-오메가( Ω(n) ) : 최선일 때(best case)의 연산 횟수를 나타낸 표기법
- 빅 - 세타( θ(n) ) : 보통일 때(average case)의 연산 횟수를 나타낸 표기법
- 빅 - 오 ( O(n) ) : 최악일 때(worst case)의 연산 횟수를 나타낸 표기법
코딩 테스트에서는 어떤 시간 복잡도 유형을 사용해야 할까?
코딩 테스트에서는 빅-오 표기법을 기준으로 수행시간을 계산하는 것이 좋습니다.
실제 코딩 테스트에서는 1개의 테스트 케이스로 해당 코드의 합-불여부를 판단하지 않습니다.
다양한 테스트 케이스를 수행해 모든 케이스를 통과 해야만 합격으로 판단하므로, 시간 복잡도 판단 시, 최악의 경우를 염두에 둬야 합니다.
알고리즘 선택의 기준으로 빅-오 표기법 사용하기
버블 정렬과 병합 정렬에 대해 알고 있고, 각각의 시간복잡도에 대해 알고 있다고 가정하고 설명하겠습니다.(각각 O($n^2$), O(nlogn) )
문제는 백준 2750번 수 정렬하기 문제 입니다.
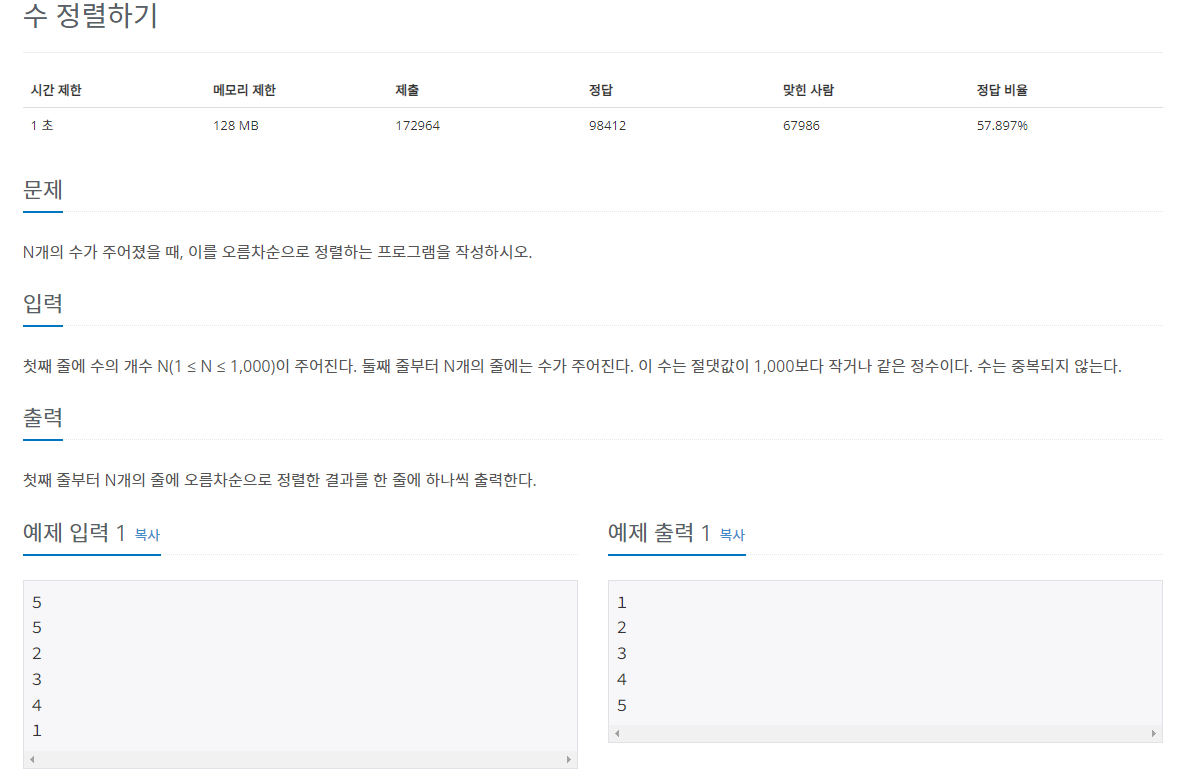
위 문제의 시간 제한이 1초이므로 이 조건을 만족하려면 1억번 이하의 연산 횟수로 문제를 해결해야 합니다. 따라서 문제에서 주어진 시간 제한과 데이터 크기를 바탕으로 어떤 정렬 알고리즘을 사용해야 할 것인지를 판단할 수 있습니다.
- 연산 횟수 = 알고리즘 시간 복잡도 X 데이터 크기
위 공식을 토대로 알고리즘이 문제에 적합한지 알아 보겠습니다.
- 버블 정렬 = $(1,000,000)^2$ = 1,000,000,000,000 > 100,000,000 → 부적합한 알고리즘
- 병합 정렬 = 1,000,000log(1,000,000) = 약 2,000,0000 < 100,000,000 → 적합한 알고리즘
버블 정렬은 약 10억번의 연산 횟수가 필요하므로, 이 문제를 풀기에 적합한 알고리즘이 아니라고 판단할 수 있습니다. 병합 정렬은 약 2,000만번의 연산 횟수로 답을 구할 수 있으므로 문제를 풀기에 적합한 알고리즘이라고 판단할 수 있습니다.
이와 같이 시간 복잡도 분석으로 문제에서 사용할 알고리즘을 선택할 수 있고, 이 과정을 바탕으로 문제를 어떻게 풀어나갈지 실마리를 찾을 수 있습니다.
시간 복잡도를 바탕으로 코드 로직 개선하기
시간 복잡도 도출 기준
- 상수는 시간 복잡도 계산에서 제외한다.
- 가장 많이 중첩된 반복문의 수행 횟수가 시간 복잡도의 기준이 된다.
이 말이 어려울 수도 있는데, 한 코드내에서 반복문이 여러번 반복 된다고 해도, 해당 반복문의 중첩이 1번인 경우에는, O(n)이지 O($n^3$)이 아니라는 말 입니다.